patch是用来构建多边形的一个基本函数。
用法一
patch(X,Y,C)
patch(X,Y,Z,C)
patch('XData',X,'YData',Y)
patch('XData',X,'YData',Y,'ZData',Z)
1.1 说明
patch(X,Y,C)用来构建一个或者多个可填充的多边形,其使用X和Y作为每个点的坐标值,patch将会按顺序连接每个点。如果要得到一个多边形,将X和Y设置为向量;如果要得到多个多边形,将X和Y设置为矩阵,没一列对应一个多边形。C决定多边形的颜色,可以是系统认定的字符,也可以是一个数值,也可以是RGB向量。
patch(X,Y,Z,C)用来构建三维坐标下的多边形。
patch(‘XData’,X,’YData’,Y)和patch(‘XData’,X,’YData’,Y,’ZData’,Z)的用法与patch(X,Y,C)和patch(X,Y,Z,C)的用法类似,只是不设定颜色。
1.2 例子
1.2.1
x = [0 1 1 0];
y = [0 0 1 1];
patch(x,y,'red')
x和y都是1*4的向量,表示将四个点(0,0)、(1,0)、(1,1)和(0,1)依次连接,最后闭合形成一个四边形,设定颜色为红色。
1.2.2
x2 = [2 5; 2 5; 8 8];
y2 = [4 0; 8 2; 4 0];
patch(x2,y2,'green')
x2和y2都是3*2的向量,两列表示画两个多边形。第一个多边形连接的点依次是(2,4)、(2,8)和(8,4),第二个多边形连接的点依次是(5,0)、(5,2)和(8,0),颜色设定为绿色。
1.2.3
如果上例的三角形第一个是红色,第二个是绿色,那么patch代码修改为
x2 = [2 5; 2 5; 8 8];
y2 = [4 0; 8 2; 4 0];
patch(x2(:,1),y2(:,1),'red')
patch(x2(:,2),y2(:,2),'green')
1.2.4
如果C是向量,并且它的大小和多边形个数相同,则每个值代表一个多边形整个面的颜色值。然后可以通过colormap改变值的颜色。例如只设定上例画不同的颜色。
x2 = [1 3; 2 2; 2 2];
y2 = [0 0; 0 0; 2 2];
c = [0; 1];
patch(x2,y2,c)
colormap(jet)
1.2.5
如果C是矩阵,并且它的维度应该和X、Y一样,每个值代表多边形端点的值,其他地方的值通过插值进行自动替换。然后可以通过colormap改变值的颜色。例如画一个渐变色对称的等腰三角形。
x2 = [1 3; 2 2; 2 2];
y2 = [0 0; 0 0; 2 2];
c = [0 0;1 1; 2 2];
patch(x2,y2,c)
colormap(jet)
1.2.6
此用法也不可以用来创建颜色渐变的曲线,只需要将y的最后一个值设为NaN,那么此多边形就不会封闭。然后设置每个点的值,用colorbar显示对应的颜色。
x = linspace(1,10,15);
y = sin(x);
y(end) = NaN;
c = y;
patch(x,y,c,'EdgeColor','interp','Marker','o','MarkerFaceColor','flat'); colormap(jet), colorbar;
其中Marker为’o’,是点的标记方式,和plot函数中的用法类似。
用法二
patch('Face',F,'Vertices',V)
2.1 说明
上述命令可以创建一个或者多个多边形,其中V的值代表点,F的值决定对哪些点进行连接。在V中每行指定一个点。如果要得到一个多边形,F仅作为一个向量;如果要得到多个多边形,F的每行表示一个多边形,行数就是多边形的个数。形成的每个多边形并不一定要有相同数量的点,为了得到不同数量的点的多边形,F的值可以设置为NaN。
2.2 例子
2.2.1
v = [0 0; 1 0; 1 1; 0 1];
f = [1 2 3 4];
patch('Faces',f,'Vertices',v,'FaceColor','red')
v表示了四个点(0,0)、(1,0)、(1,1)和(0,1),这些点的序号按自然数排列。f将按其向量中点的顺序依次连接,最后闭合成面。面的颜色设置为红色。
2.2.2
如果将上例中点的连接顺序改变将得到不同的多边形。
v = [0 0; 1 0; 1 1; 0 1];
f = [1 2 4 3];
patch('Faces',f,'Vertices',v,'FaceColor','blue')
2.2.3
如果要画1.2.2中同样的图形,则代码为
v2 = [2 4; 2 8; 8 4; 5 0; 5 2; 8 0];
f2 = [1 2 3; 4 5 6];
patch('Faces',f2,'Vertices',v2,'FaceColor','green')
v2中定义了六个点,f2分别将第1、2、3个点闭合,将第4、5、6个点闭合。面的颜色设置为绿色。
2.2.4
和1.2.4类似,如果C是向量,并且它的大小和多边形个数相同,则每个值代表一个多边形整个面的颜色值。然后可以通过colormap改变值的颜色。
v2 = [1 0;2 0;2 2;3 0; 2 0;2 2];
f2 = [1 2 3;4 5 6]; c = [0; 1];
patch('Faces',f2,'Vertices',v2,'FaceVertexCData',c,'FaceColor','flat');
colormap(jet)
此时,’FaceColor’的值为’flat’。
2.2.5
如果C是向量,并且它的大小和点的个数相同,则每个值代表每个点的颜色,其他地方通过插值得到颜色值。那么得到和1.2.5中的图形一样的效果,代码如下:
v2 = [1 0;2 0;2 2;3 0; 2 0;2 2];
f2 = [1 2 3;4 5 6];
c = [0; 1; 2; 0; 1; 2];
patch('Faces',f2,'Vertices',v2,'FaceVertexCData',c,'FaceColor','interp');
colormap(jet)
此时,’FaceColor’的值为’interp’。
2.2.6
如果不要填充颜色,只要边框,只需要修改patch的设定参数’FaceColor’为’none’。
v = [0 0; 1 0; 1 1];
f = [1 2 3];
figure
patch('Faces',f,'Vertices',v,'EdgeColor','green','FaceColor','none','LineWidth',2);
2.2.7
如果要设置每一边为不同的颜色,需要设置起点的颜色,并且EdgeColor为’flat’。
v = [2 0; 3 0; 3 1];
f = [1 2 3];
c = [1 0 0; % red
0 1 0; % green
0 0 1]; % blue
patch('Faces',f,'Vertices',v,'FaceVertexCData',c,'EdgeColor','flat','FaceColor','none','LineWidth',2);
2.2.8
如果要设置半透明的多变形,可以设置FaceAlpha的值在0到1之间,1表示不透明。
v1 = [2 4; 2 8; 8 4];
f1 = [1 2 3];
figure
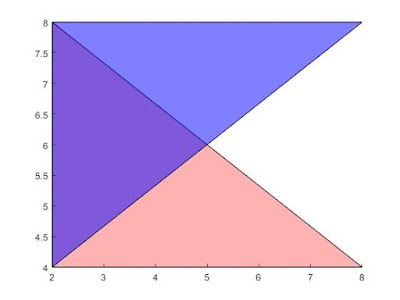
patch('Faces',f1,'Vertices',v1,'FaceColor','red','FaceAlpha',.3);
v2 = [2 4; 2 8; 8 8];
f2 = [1 2 3];
patch('Faces',f2,'Vertices',v2,'FaceColor','blue','FaceAlpha',.5);
2.2.9
要使用一维m个网格的模型来显示“油藏数值模拟中的一维水驱油”问题,假设此时的m为15,网格的颜色表示饱和度值。
NumX = 15;
VA = zeros(2*(NumX+1),2); %网格中的所有点
VA(1:(NumX+1),1) = 1:(NumX+1); %点的顺序按维度排序,一共两排
VA((NumX+2):(2*(NumX+1)),1) = 1:(NumX+1);
VA((NumX+2):(2*(NumX+1)),2) = 1;
FA = zeros(NumX,4); %网格中的所有块
FA(:,1) = 1:NumX; %依次将四个点连接组成四边形网格
FA(:,2) = 2:(NumX+1);
FA(:,3) = (NumX+3):(2*NumX+2);
FA(:,4) = (NumX+2):(2*NumX+1);
Sw = (1:-1/14:0)';
patch('Faces',FA,'Vertices',VA,'FaceVertexCData',Sw,'FaceColor','flat','Edgecolor','none');
colormap(jet),colorbar
xlim([1 (NumX+1)])
set(gca,'ytick',[0 1])
set(gca,'yticklabel',{'0','1'})
xtk = 1:(NumX+1);
set(gca,'xtick',xtk)
2.2.10
要使用一个m*n的网格模型来显示“油藏数值模拟中的二维水驱油”问题,假设此时的m为15,n为10,网格的颜色表示饱和度值。
m = 15;
n = 10;
VA = zeros((n+1)*(m+1),2); %网格中的所有点,一共有(n+1)*(m+1)个才能围成m*n个网格
for j = 1:(n+1) %点的顺序按m的正方向排序,一共n+1排
VA(((j-1)*(m+1)+1):(j*(m+1)),1) = 1:(m+1);
VA(((j-1)*(m+1)+1):(j*(m+1)),2) = j;
end FA = zeros(m*n,4); %网格中的所有块
for j = 1:n %依次将四个点连接组成四边形网格
for i = 1:m
FA(((j-1)*m+i),1) = (j-1)*(m+1) + i;
FA(((j-1)*m+i),2) = (j-1)*(m+1) + i +1;
FA(((j-1)*m+i),3) = j*(m+1) + i + 1;
FA(((j-1)*m+i),4) = j*(m+1) + i;
end
end
Sw = rand(m*n,1);
patch('Faces',FA,'Vertices',VA,'FaceVertexCData',Sw,'FaceColor','flat','Edgecolor','none');
colormap(jet),colorbar
xlim([1 (m+1)])
ylim([1 (n+1)])
用法三
patch(S)
3.1 说明
使用“结构”S(类似与高级程序语言中的类)创建一个或者多个多边形,S的域对应patch函数的属性,S的域值对应patch函数的属性值。
3.2 例子
3.2.1
clear S
S.Vertices = [2 4; 2 8; 8 4; 5 0; 5 2; 8 0];
S.Faces = [1 2 3; 4 5 6];
S.FaceVertexCData = [0; 1];
S.FaceColor = 'flat';
S.EdgeColor = 'red';
S.LineWidth = 2;
figure
patch(S)
结语
通过查看MatLab帮助文档和自己的画图实践,翻译或总结出了以上用法和例子,编写过程中难免有失误,敬请原谅和指导。
以上只是个人认为的patch基本用法,若今后遇到更高级的用法,还将继续总结。
以上只是个人认为的patch基本用法,若今后遇到更高级的用法,还将继续总结。













Thank you!
ReplyDelete